El teorema de Pitágoras es uno de los conceptos fundamentales de la geometría que establece la relación entre los lados de un triángulo rectángulo. Este teorema dice que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. En este artículo, exploraremos cómo se puede demostrar el teorema de Pitágoras utilizando acrílico, un material versátil y duradero.

¿Qué es el acrílico?
El acrílico es un tipo de plástico transparente y resistente que se utiliza en una amplia variedad de aplicaciones, desde ventanas y paneles de automóviles hasta muebles y accesorios de decoración. Este material es conocido por su alta resistencia al impacto y su capacidad para transmitir la luz de manera eficiente, lo que lo convierte en una excelente opción para demostraciones visuales.
La demostración en acrílico
Para demostrar el teorema de Pitágoras utilizando acrílico, necesitaremos algunos elementos básicos:
- Un trozo de acrílico transparente
- Una regla
- Un lápiz
- Una sierra para cortar acrílico
Para comenzar, trazaremos un triángulo rectángulo en el acrílico utilizando la regla y el lápiz. Asegúrate de que los ángulos del triángulo sean de 90 grados, ya que esto es esencial para la demostración del teorema de Pitágoras.
Luego, utilizando la sierra para cortar acrílico, cortaremos el triángulo a lo largo de los lados del cateto y la hipotenusa. Esto nos permitirá manipular las piezas de manera independiente y facilitar la demostración.
Ahora, colocaremos las tres piezas del triángulo rectángulo en una superficie plana, de modo que los catetos formen un ángulo recto y la hipotenusa esté alineada con ellos. Asegúrate de que las piezas estén bien alineadas y en contacto entre sí.
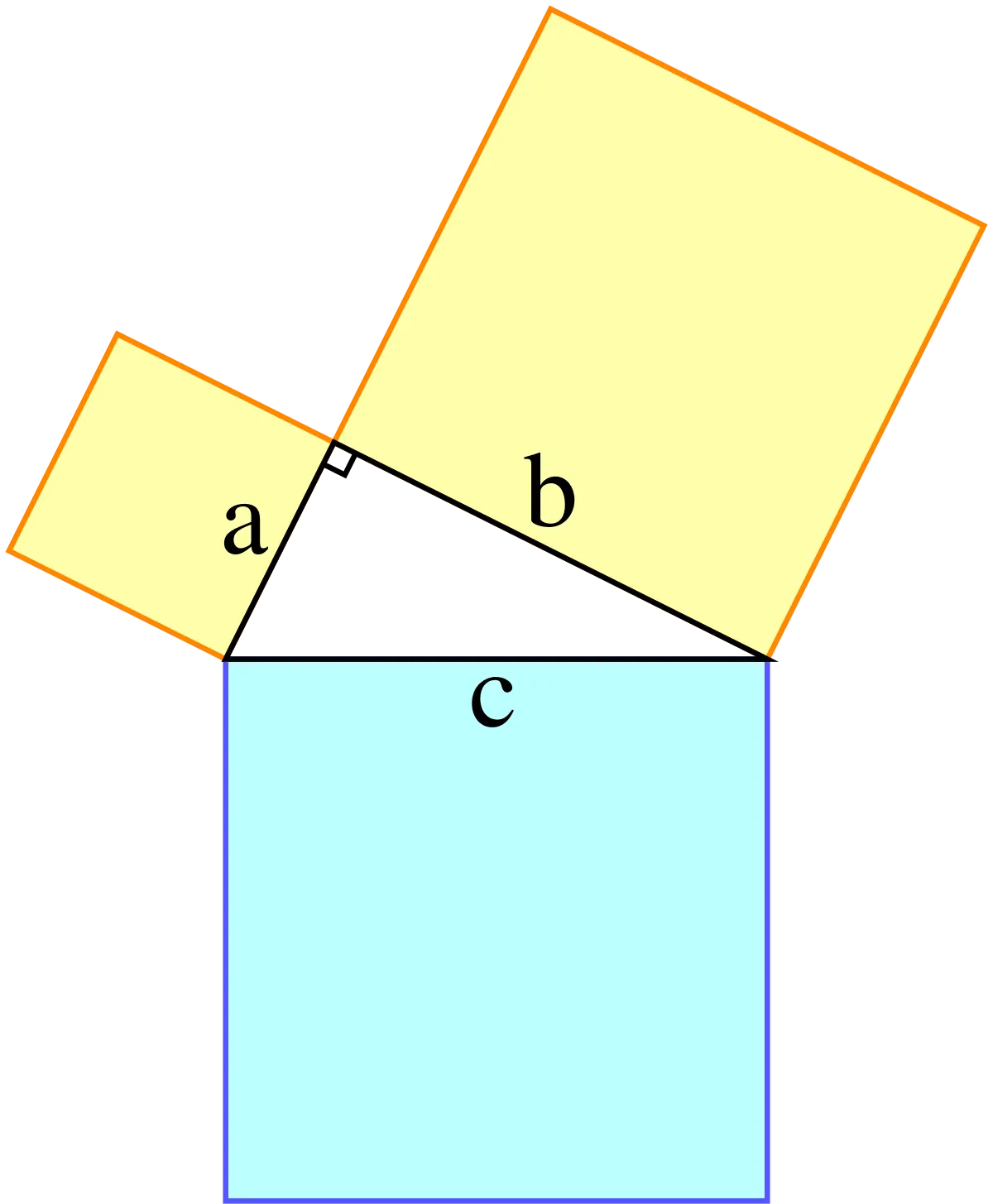
Una vez que hayamos colocado las piezas en la posición correcta, podemos observar claramente cómo se cumple el teorema de Pitágoras. La suma de los cuadrados de los catetos (las áreas de las piezas) es igual al cuadrado de la hipotenusa (el área de la pieza completa).
Beneficios de la demostración en acrílico
La demostración del teorema de Pitágoras utilizando acrílico tiene varios beneficios:
- Es visualmente atractiva y fácil de comprender, lo que la hace ideal para enseñar a estudiantes y personas interesadas en la geometría.
- El acrílico es un material duradero y resistente, lo que garantiza que la demostración se pueda utilizar durante mucho tiempo sin dañarse.
- El acrílico transparente permite ver claramente las diferentes partes del triángulo rectángulo y cómo se relacionan entre sí.
- Es una forma práctica de demostrar el teorema de Pitágoras sin la necesidad de utilizar papel y lápiz.
La demostración del teorema de Pitágoras en acrílico es una forma efectiva y visualmente atractiva de enseñar este concepto fundamental de la geometría. El uso de acrílico transparente permite una fácil visualización de las partes del triángulo rectángulo y cómo se relacionan entre sí. Además, el acrílico es un material duradero y resistente que garantiza que la demostración se pueda utilizar durante mucho tiempo. ¡Anímate a utilizar esta demostración en tus clases o estudios de geometría!
Consultas habituales
¿Dónde puedo conseguir acrílico?
El acrílico se puede encontrar en tiendas de materiales de construcción, tiendas de artesanía y en línea. Asegúrate de elegir un grosor adecuado para la demostración del teorema de Pitágoras.
¿Necesito habilidades especiales para cortar el acrílico?
No es necesario tener habilidades especiales para cortar el acrílico, pero se recomienda utilizar una sierra específica para este material y seguir las instrucciones de seguridad adecuadas.
¿Existen otros materiales que pueda utilizar para la demostración del teorema de Pitágoras?
Sí, además del acrílico, puedes utilizar papel, cartón o incluso modelos tridimensionales para demostrar el teorema de Pitágoras. La elección del material depende de tus preferencias y recursos disponibles.
¿Hay otras aplicaciones del acrílico en la geometría?
Sí, el acrílico se utiliza ampliamente en la geometría para la construcción de modelos tridimensionales, paneles de visualización y otros recursos visuales. Su transparencia y durabilidad lo convierten en una excelente opción para estas aplicaciones.
Si te ha interesado Demostración del teorema de pitágoras en acrílico, te invitamos a explorar más sobre plásticos, policarbonatos y acrílicos en nuestra categoría Plásticos.

